
Возведение матрицы в степень онлайн
|

|
Возведение матрицы в степень представляет собой умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу.
Так как в общем случае при умножении матриц должно выполняться равенство количества столбцов первой матрицы и количества строк второй матрицы, получается, что при умножении матрицы саму на себя в ней должно быть равное количество строк и столбцов.
Отсюда вытекает правило: допускается возводить в степень только квадратные матрицы, то есть с равным количеством строк и столбцов.
Получается, что возведение матрицы в степень – это частный случай умножения матриц по свойству ассоциативности матричного умножения.
Математически это можно представить следующим образом:
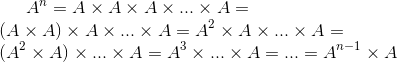
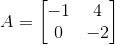
Решение.
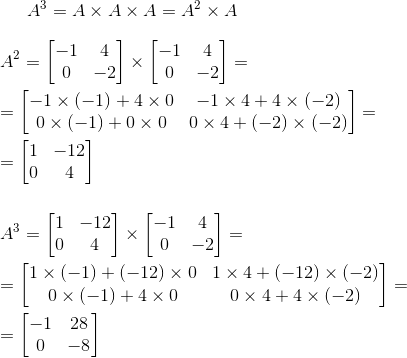
в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x
(например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.