Умножение матрицы на матрицу онлайн

Умножение матрицы на матрицу

Операция умножения двух матриц А и В представляет собой вычисление результирующей матрицы С, каждый элемент cij которой равен сумме произведений элементов в соответствующей строке первой матрицы aik и элементов в столбце второй матрицы bkj.

Две матрицы можно умножать между собой только тогда, когда количество столбцов в первой матрице совпадает с количеством строк во второй матрице. Другими словами первая матрица обязательно должна быть согласованной со второй матрицей. Таким образом, результатом операции умножения матрицы размера m×n на матрицу размером n×k является матрица размером m×k.

Итак, произведение матрицы Аm×n на матрицу Вn×k – это матрица Сm×k, элемент cij которой, находящийся в i-ой строке и j-ом столбце, равен сумме произведений i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В.

Каждый элемент матрицы Сm×k равен:

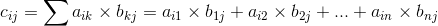
где k принимает значение от 1 до n.

Рассмотрим пример умножения двух матриц.

Даны две матрицы А и В.

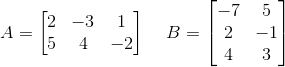
Найти произведение матриц А × В.
Решение.

Свойства умножения матриц (свойства справедливы, если матрицы подходящего порядка):

1. Ассоциативность
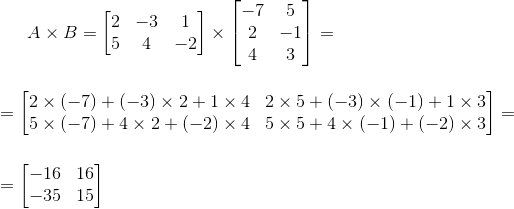
   (А × В) × С = А × (В × С)
2. Дистрибутивность
   А × (В+С) = А×В + А×С
(А+В) × С = А×С + В×С
3. Ассоциативность и коммутативность относительно умножения на число
   (k×A) × B = k × (A×B) = A × (k×B)
4. В общем случае умножение матриц не коммутативно
   А×В ≠ В×А
5. Произведение коммутативно в случае умножения на единичную матрицу
   Em × Am×n = Am×n × En = Am×n

Решение